Level shifting

• ‘Level shifting’

• Given any set \(S\), there is a set \(\mathbf{Rel}(S)\) of binary relations on \(S\) (i.e. ?\(\mathbb{P}(S \times S)\))

• This power set can be given a preorder structure using the ?subset relation.

• A subset of possible relations satisfy the axioms of preorder relations. \(\mathbf{Pos}(S) \subseteq \mathbb{P}(S \times S)\) which again inherits a preorder structure from the subset relation

  • A ?preorder on the possible preorder structures of \(S\), that’s a level shift.

• The inclusion map \(\mathbf{Pos}(S) \hookrightarrow \mathbf{Rel}(S)\) is a right adjoint to a Galois connection, while its left adjoint is \(\mathbf{Rel}(S)\overset{Cl}{\twoheadrightarrow} \mathbf{Pos}(S)\) which takes the ?reflexive and transitive closure of an arbitrary relation.

Let \(S=\{1,2,3\}\)

1. Come up with any preorder relation on \(S\), and define \(U(\leq):=\{(s_1,s_2)\ |\ s_1 \leq s_2\}\) (the relation ‘underlying’ the preorder. Note \(\mathbf{Pos}(S) \xhookrightarrow{U} \mathbf{Rel}(S)\))

2. Pick binary relations such that \(Q \subseteq U(\leq)\) and \(Q' \not \subseteq U(\leq)\)

We want to check that the reflexive/transitive closure operation \(Cl\) is really left adjoint to the underlying relation \(U\).

• The meaning of \(Cl \dashv U\) is \(Cl(R) \sqsubset \leq \iff R \sqsubset U(\leq)\), where \(\sqsubset\) is the order relation on \(\mathbf{Pos}(S)\)

1. Concretely show that \(Cl(Q) \sqsubset \leq\)

2. Concretely show that \(Cl(Q') \not \sqsubset \leq\)

Solution(1)

1. Let the preorder be given by this diagram (with implicit reflexive arrows):

   

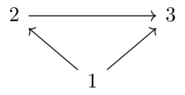
2. Let \(Q\) be given by the following diagram

   • 

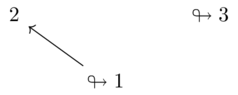
   • and let \(Q'=S\times S\)

3. ?\(Cl(Q) = \{11,12,22,33\}\) \(\sqsubset\) ?\(\leq = \{11,22,33,12,23,13\}\)

4. ?\(Cl(Q') = Q' = S \times S\) \(\not \sqsubset\) ?\(\leq\) (reason: ?\((3,1) \in S \times S\) but \((3,1) \not \in \leq\))